Daty zajęć w maju
Maj to miesiąc, w którym jest wiele przerw. U nas jednak w maju będzie się działo więcej niż zwykle. I tak:
-
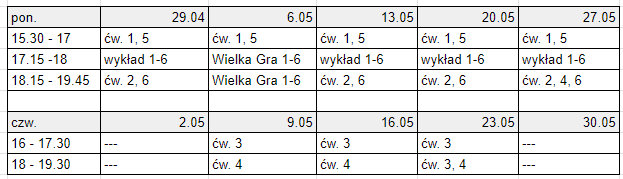
w poniedziałek 29 kwietnia wszystkie zajęcia odbywają się wg zwkłego planu,
-
w czwartek 2 maja nie ma zajęć,
-
w poniedziałek 6 maja ćwiczenia grup 1 i 5 odbywają się jak zwykle o godz. 15.30; a o godz. 17.15 rozpoczynamy Wielką Grę, na którą zaproszeni są wszyscy uczestnicy ze wszystkich grup 1-6 (będzie można wygrać dodatkowe punkty - wszystkie miejsca są punktowane),
-
od 9 do 23 maja wszystkie zajęcia odbywają się jak zwykle,
-
w poniedziałek 27 maja wykład i ćwiczenia grup 1, 2, 5, 6 odbywają się jak zwykle, dodatkowo będą wtedy również ostatnie ćwiczenia grupy 3 (godz. 15.30) i grupy 4 (godz. 18).
-
w czwartek 30 maja nie ma zajęć (Boże Ciało).
Do zobaczenia i dobrej majówki!
Kolejne, częściowe wyniki rywalizacji XV edycji
Rywalizacja nie jest głównym celem naszego projektu, ale wiemy, że dla wielu jest emocjonująca. Ogłaszamy drugą odsłonę wstepnych jej wyników. Tegoroczna czołówka szkół odbiega znacznie od tych z poprzednich edycji, gratulujemy tym, którzy pracują na dobre imię swojej szkoły.
Na razie nieco dyskryminowani (przez mniejszą liczbę zajęć) są uczestnicy grup 1 i 5 - ale to wyrówna się w maju, oczekujemy wtedy wielu zaskoczeń! Wyniki te mogą też nie brać pod uwagę wszystkich oddanych przez Was prac, jeśli nie zostały one jeszcze sprawdzone.
Przypominamy, że wszystko może się zmienić! (Nie, nie będziemy już zdobytych punktów odbierać - ale może ktoś inny zdobędzie ich więcej?). Wszystko zależy od Waszej dalszej aktywności. Pozdrawiamy serdecznie tych, którzy lubią rywalizację, i tych, którzy jej nie lubią. Pamiętamy także o Was.
- Rywalizacja szkół
- Czołówka punktowej rywalizacji indywidualnej
- Czołówka rywalizacji krówkowej
Gratulujemy wszystkim!
Gdyby ktoś sobie nie życzył, żeby publikować jego imię i nazwisko w tej rywalizacji, prosimy o wiadomość.

Wielkanoc
Wszystkim naszym Uczestnikom, ich Nauczycielom, Rodzicom, wszystkim Prowadzącym nasze zajęcia teraz i onegdaj, a także Sympatykom - wszystkim życzymy najlepszych z dotychczasowych Świąt Wielkanocnych! Oczywiście życzymy muzycznie - oto nad czym ostatnio pracowaliśmy na zajęciach.
Zakończylismy rekrutację na XV edycję
20 lutego zakończylismy rekrutację na XV edycję Matematyki dla Ciekawych Świata. Dziękujemy i Uczniom, i Nauczycielom, i Rodzicom za zainteresowanie. Przyjęliśmy 126 osób. Każda zgłoszona osoba powinna otrzymać (27 lutego) wiadomość mailową z wynikami rekrutacji. Przesłaliśmy też wskazówki co do dotarcia na miejsce i instrukcję dotyczącą naszego serwera na discordzie. Do zobaczenia wkrótce! Życzymy Wam i sobie bardzo udanej XV edycji!





